ジェネレーター読み替え操作
マッピング行列の標準形はレギュラーテンペラメントを一意に識別する方法として重要だが、それ以外の形式が不要なわけではない。同じテンパーされた音程を生成するのであっても異なる表現を取りたい人もいるからである。いくつかのそういう形式が存在していて、positive generator form、equave-reduced generator form、minimal-generator formなどである。
本項目では、標準形としてdefactoredエルミート標準形を採用していることにする。二つのマッピングが等価である、つまり標準形が一致しゆえに同じテンペラメントを表している場合、対応するジェネレーター基底も等価である。これはジェネレーターのサイズが一致しているという意味ではなく、それぞれのジェネレーターの組が基底となって最終的に同じピッチ集合を生成するということである。
例として、5リミットミーントーンのよく挙げられる形は [⟨1 1 0] ⟨0 1 4]⟩ であり、この形の場合は2つのジェネレーターは大まかにオクターブと完全5度となる(なぜマッピングを見ただけでそれがわかるのか?→マッピングの1列目を見れば 2/1 を最初のジェネレーター1個で表すことが読み取れ、またまともなチューニングアルゴリズムならこのジェネレーターを 2400 セントとかではなくだいたい 1200 セントにチューニングするはずである。2個目は以下略)。しかしオクターブと完全5度の組み合わせでできるピッチ集合はオクターブと完全4度の組み合わせでも問題なく生成できる。具体的には、完全5度1個で到達できるピッチにはオクターブ上がって完全4度下がることによっても到達できるからである。なので5リミットミーントーンをオクターブと完全4度で組み立てるというシチュエーションの下では、マッピングを [⟨1 2 4] ⟨0 -1 -4]⟩ と書けるとよい。
そして、エルミート標準形はジェネレーターがなるべく(単音程化しない)素数音程になるようにするものであり、ミーントーンのマッピングをジェネレーターがオクターブと完全12度(トリターブ、3/1)の組み合わせになるように書けるとよい。完全5度1個で到達できるピッチには完全12度上がってオクターブ下がることによっても到達できるのでこれも問題なく行え、マッピングとして [⟨1 0 -4] ⟨0 1 4]⟩ が得られる。
| [octave-count fifth-count⟩ | [⟨1 1 0] ⟨0 1 4]⟩ |
|---|---|
| [octave-count fourth-count⟩ | [⟨1 2 4] ⟨0 -1 -4]⟩ |
| [octave-count tritave-count⟩ | [⟨1 0 -4] ⟨0 1 4]⟩ |
これら3つのマッピングの形式が相互に関係していそうで、実際にそうなのだが、正確にどういうことなのかは一見しただけではよくわからない。本項目の目的はこれらを相互に変換する操作を実演し、操作がこれらの関係をどう説明するかを理解することである。
ジェネレーターを変形させる操作
用いるのは行に関する行列の基本変形のうち行列式の絶対値が変化しないものである。行列式の絶対値が変化する操作により得られるマッピングは等価なものとはみなされない。任意の行を1より大きい整数倍するとマッピングをenfactorすることになり、ある行の最大公約数が1より大きくて割ることができる場合このマッピングがすでにenfactoredだったことが判明する。
操作その1: あるジェネレーターをほかのあるジェネレーターのサイズ分変化させる
マッピング [math]\displaystyle{ M }[/math] の各行を [math]\displaystyle{ 𝒎_1, 𝒎_2 ... 𝒎_r }[/math]、それぞれに対応するジェネレーターを [math]\displaystyle{ g_1, g_2 ... g_r }[/math] と書くことにして、[math]\displaystyle{ g_a }[/math] を [math]\displaystyle{ g_b }[/math] 分だけ増加させたい場合、[math]\displaystyle{ 𝒎_b }[/math] を [math]\displaystyle{ 𝒎_b' = 𝒎_b - 𝒎_a }[/math] で置き換える。
先ほどの最後の例、「オクターブと完全12度の組み合わせによるミーントーン」で考えてみよう。スタート地点を [⟨1 1 0] ⟨0 1 4]⟩ とすると、ジェネレーターは順番にオクターブと完全5度となる。2番目のジェネレーターを1番目のジェネレーターの分だけ延ばすと完全12度となる。記号で書くと [math]\displaystyle{ g_2 }[/math] を [math]\displaystyle{ g_2 + g_1 }[/math] に変更したい。上記操作に従えば、[math]\displaystyle{ 𝒎_1 }[/math] を [math]\displaystyle{ 𝒎_1' = 𝒎_1 - 𝒎_2 }[/math] で置き換える。[math]\displaystyle{ 𝒎_1' }[/math] は次のようになる:
[math]\displaystyle{ \begin{array} {r} 𝒎_1 \\ -𝒎_2 \\ \hline 𝒎_1' \end{array} → \begin{array} {r} & \langle & 1 & 1 & 0 & ] \\ - & \langle & 0 & 1 & 4 & ] \\ \hline & \langle & 1 & 0 & -4 & ] \end{array} }[/math]
そして1行目を差し替えて [⟨1 0 -4] ⟨0 1 4]⟩ が得られる。
マッピングの書き換えた行(1行目)とサイズが変化するジェネレーター(2番目)が対応しないことを不思議に感じるかもしれない。2次元格子で位置を特定するのにそれぞれのジェネレーターを適切に組み合わせる必要があることを思い出してほしい。この操作でマッピングの1行目が担っていた情報はほかの行に漏れていない。1行目だけで処理されていた音程は書き換え後もほかの行からは手伝いようがない。(本例ではマッピングの最初の列を見れば 2/1 をマッピングする仕事が変化していないのが明らかである。)マッピングが同じピッチ集合を生成するためには、少なくとも1番目のジェネレーターのサイズを変更できないだろうことがわかる。逆に情報を漏らした2行目は結果として自分の仕事を漏洩先に手伝わせることになるので、自分の力加減(2番目のジェネレーターのサイズ)を調整する必要が出てくる。(本例ではマイナスにして漏らしているのでむしろ漏洩先からの協力が減って2行目ががんばることになる。3/1 をマッピングするとき両方のジェネレーターが協力してオクターブ1個と完全5度1個を積み上げていたのが、書き換え後は2番目のジェネレーターがオクターブと完全5度のセット=完全12度となる。)
等価なマッピングであることが表現できるように等号で書くと、
[math]\displaystyle{ \begin{align} \left(\begin{array}{c} \mathrm{octave} \\ \mathrm{fifth} \end{array} \right) &= \left(\begin{array}{ccc} 1 & 1 & 0 \\ 0 & 1 & 4 \end{array} \right) \left( \begin{array}{c} p_2 \\ p_3 \\ p_5 \end{array} \right) \\ &= \left(\begin{array}{cc} 1 & 1 \\ 0 & 1 \end{array} \right) \left(\begin{array}{cc} 1 & -1 \\ 0 & 1 \end{array} \right) \left(\begin{array}{ccc} 1 & 1 & 0 \\ 0 & 1 & 4 \end{array} \right) \left( \begin{array}{c} p_2 \\ p_3 \\ p_5 \end{array} \right) \\ &= \left(\begin{array}{cc} 1 & 1 \\ 0 & 1 \end{array} \right) \left(\begin{array}{ccc} 1 & 0 & -4 \\ 0 & 1 & 4 \end{array} \right) \left( \begin{array}{c} p_2 \\ p_3 \\ p_5 \end{array} \right) \\ \end{align} }[/math]
右辺の最初の(1 1; 0 1)はgenerator tuning mapに作用することでジェネレーターのサイズを変換する。
[math]\displaystyle{ \begin{align} \left( \mathrm{octavesize} \ \mathrm{fifthsize} \right) \left(\begin{array}{cc} 1 & 1 \\ 0 & 1 \end{array} \right) &= \left( \mathrm{octavesize} \ \mathrm{tritavesize} \right) \end{align} }[/math]
よって
[math]\displaystyle{ \begin{align} \mathrm{temperedintervalsize} &= \left( \mathrm{octavesize} \ \mathrm{fifthsize} \right) \left(\begin{array}{c} \mathrm{octave} \\ \mathrm{fifth} \end{array} \right) \\ &= \left( \mathrm{octavesize} \ \mathrm{fifthsize} \right) \left(\begin{array}{ccc} 1 & 1 & 0 \\ 0 & 1 & 4 \end{array} \right) \left( \begin{array}{c} p_2 \\ p_3 \\ p_5 \end{array} \right) \\ &= \left( \mathrm{octavesize} \ \mathrm{tritavesize} \right) \left(\begin{array}{ccc} 1 & 0 & -4 \\ 0 & 1 & 4 \end{array} \right) \left( \begin{array}{c} p_2 \\ p_3 \\ p_5 \end{array} \right) \\ \end{align} }[/math]
反対に、もし [math]\displaystyle{ g_a }[/math] を [math]\displaystyle{ g_b }[/math] 分だけ減少させたい場合、[math]\displaystyle{ 𝒎_b }[/math] を [math]\displaystyle{ 𝒎_b' = 𝒎_b }[/math] 足す [math]\displaystyle{ 𝒎_a }[/math] で置き換える。
操作その2: ジェネレーターの符号反転
よりややこしい例、完全5度で組み立てられたミーントーンから完全4度で組み立てられたミーントーンへの変換を考えよう。再確認すると、完全4度は完全5度の相補音程(転回音程)なのでこれは当然可能である。
この相補音程化が常にできるというのはオクターブに限った話ではない。ジェネレーターをそれに対するもう一方のジェネレーターの相補音程に置き換えて同じピッチ集合を記述できる。
この相補音程に置き換えるというのを手順にまとめると: まずそのジェネレーターの符号を反転し(操作その2)、次にそれにもう一方のジェネレーターを加える(操作その1)。(まずもう一方のジェネレーターを引いて(操作その1の反対バージョン)、引きすぎてジェネレーターの大きさが負になってしまったので符号を反転する(操作その2)のでもよい。)
なので、最初のステップはミーントーンを特徴づけるジェネレーターの符号を反転し、完全5度上ではなく完全5度下を表すようにすることである。
これは先ほどの操作その1では達成できない。操作その1では2つの別々のジェネレーターが必要だった。(操作その1は行列の基本変形の中でも行列式が変化しないものだが、それをむりやり1行で実行すると行列式が(n+1)倍されるようになって性質が違いすぎるので、そんなものは別の基本変形であると位置づけられる。)
幸運なことに操作その2はかなり簡単である。[math]\displaystyle{ g_a }[/math] を反転させたいなら、[math]\displaystyle{ 𝒎_a }[/math] の全項の符号を反転する。本例なら [math]\displaystyle{ 𝒎_2 = }[/math] ⟨0 1 4] を [math]\displaystyle{ 𝒎_2' = }[/math] ⟨0 -1 -4] で置き換え、[⟨1 1 0] ⟨0 -1 -4]⟩ を得る。
次のステップは操作その1で負の完全5度にオクターブを加えて正の完全4度に変換することである。そのために、[math]\displaystyle{ 𝒎_1 }[/math] を [math]\displaystyle{ 𝒎_1 - 𝒎_2' }[/math] で置き換える。
[math]\displaystyle{ \begin{array} {r} 𝒎_1 \\ -𝒎_2' \\ \hline 𝒎_1' \end{array} → \begin{array} {r} & \langle & 1 & 1 & 0 & ] \\ - & \langle & 0 & -1 & -4 & ] \\ \hline & \langle & 1 & 2 & 4 & ] \end{array} }[/math]
これにて、[⟨1 2 4] ⟨0 -1 -4]⟩ を得る。
ランク2を超えて
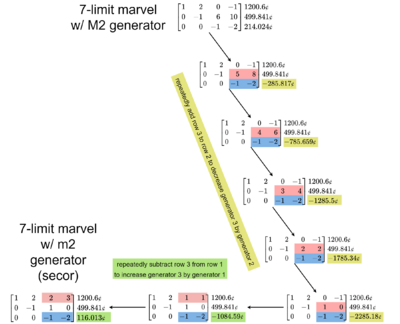
以上の2種類の操作でそのテンペラメントを正しく表せる任意のジェネレーター基底を得ることができる。そしてこれはランク2に限らず任意のランクのテンペラメントで機能する(ランク1には操作その2だけが使えて結果は自明である)。
例として、7リミットマーベルの標準形は [⟨1 0 0 -5] ⟨0 1 0 2] ⟨0 0 1 2]⟩ であり、ジェネレーターは順にオクターブ、完全12度、完全17度(5/1)となる。ここから2番目のジェネレーターを完全5度にしたい、つまり[math]\displaystyle{ g_2 }[/math] を [math]\displaystyle{ g_1 }[/math] だけ減らしたいという場合、操作その1に従って [math]\displaystyle{ 𝒎_1 }[/math] に [math]\displaystyle{ 𝒎_2 }[/math] を足す。これで [⟨1 1 0 -3] ⟨0 1 0 2] ⟨0 0 1 2]⟩ が得られる。都合のいいことに、この操作に関係しなかった3番目のジェネレーターのサイズは影響を受けない。サイズが影響を受けるのは情報を漏らした2行目だけである。
このようにジェネレーターのサイズの影響は手順ごとに局限されるので、順序だててジェネレーターのサイズを変更してゆくことができ、豊富に様々な表現方法が得られるのである。右図を参照のこと。
チューニング
positive generator form、equave-reduced generator form、minimal-generator formなどはジェネレーターのサイズに関する規定があるため、チューニングを定めてから変換を行う必要がある。この時に単純に目についた元音程を使い [math]\displaystyle{ g_1 = \mathrm{cent}(2/1), g_2 = \mathrm{cent}(3/2) }[/math] を採用するのは信頼できる方法とは言えない。採用されるチューニングはツールによっても違っているが、本項目中の例では minimax-ES チューニングを採用する。
mingen form を求める例
(mingen form を求める特定の実装の説明) See en:Generator form manipulation #Easy instructions table to achieve mingen form for rank-2 mapping