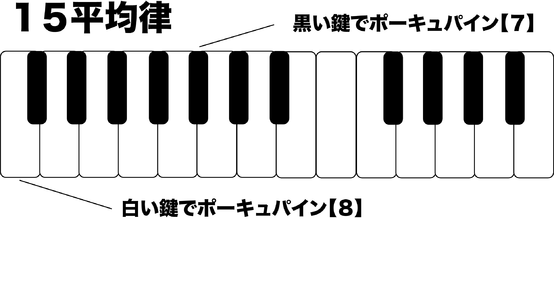
15平均律
| ← 14平均律 | 15平均律 | 16平均律 → |
音楽において、15 equal temperamentは15TETや15EDO、または15ETと呼ばれる。15平均律はオクターブを15の均等なステップに分割し、テンパーされた音階である。各ステップは周波数比 [math]\displaystyle{ 2^{1/15} }[/math] 、または80 ¢ である。5平均律が3つの音階、または3平均律が5つの音階と解釈することが可能である。
15平均律は7-リミットにもとづく音程に近いいくつかの音程を持つため、7-リミットテンペラメントとして見なすことが可能である。しかしまた、明らかに11-リミット音程に近い音程もいくつか含んでいる。ゆえに、11リミットテンペラメントとして述べることが合理的である。しかし12平均律の3度と9度の響きからは離れているため、15平均律に近いJIを探すことは、要求されているそれらのコードを避けることがベストだと考えられる。もしくは、注意深く扱う必要がある。15平均律はまた、明確なシントニックコンマ (en) を持つ5アドリミットインターバル(3/2、5/4、6/5)の表現と、異なっていると認識できる最も小さい平均律である。このことは注目に値する。
15平均律のシステムにおいて、メジャーサードは2(1200cent)を完全に分割できず、そして一般の3全音(600セント)の欠如と結びつく。このチューニングは、はじめ方向感覚を失わせる。しかしながら、ギターは12音システムギターと異なり、Eからe、または6弦から1弦のように対照的にチューニングできる。カーブを学ぶことはとても管理しやすい。すべてのコードはどこでも同じ転調のようにみえ、マイナーアルペジオは垂直に積み重ねられ、とても簡単に演奏できる。15音はたぶん誰もがより優れたハーモニーとゼンハーモニー、音数の管理のしやすさ、5平均律の重なりによる音の特徴に興味を持つ、有望な駆け出しとなる。
理論
素数倍音
| 倍音 | 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 | 31 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 誤差 | 絶対 (¢) | +0.0 | +18.0 | +13.7 | -8.8 | +8.7 | +39.5 | -25.0 | +22.5 | +11.7 | +10.4 | -25.0 |
| 相対 (%) | +0.0 | +22.6 | +17.1 | -11.0 | +10.9 | +49.3 | -31.2 | +28.1 | +14.7 | +13.0 | -31.3 | |
| ステップ (reduced) |
15 (0) |
24 (9) |
35 (5) |
42 (12) |
52 (7) |
56 (11) |
61 (1) |
64 (4) |
68 (8) |
73 (13) |
74 (14) | |
純正音程近似
純正音程のマッピング
以下の表は、15平均律で15奇数リミット音程がどのように表されるかを示している。素数倍音は太字で、非一貫的な音程は斜体で示す。
| 音程と補音程 | 誤差 (絶対, ¢) | 誤差 (相対, %) |
|---|---|---|
| 1/1, 2/1 | 0.000 | 0.0 |
| 13/9, 18/13 | 3.382 | 4.2 |
| 5/3, 6/5 | 4.359 | 5.4 |
| 11/10, 20/11 | 5.004 | 6.3 |
| 15/13, 26/15 | 7.741 | 9.7 |
| 11/8, 16/11 | 8.682 | 10.9 |
| 7/4, 8/7 | 8.826 | 11.0 |
| 11/6, 12/11 | 9.363 | 11.7 |
| 5/4, 8/5 | 13.686 | 17.1 |
| 11/7, 14/11 | 17.508 | 21.9 |
| 3/2, 4/3 | 18.045 | 22.6 |
| 13/12, 24/13 | 21.427 | 26.8 |
| 9/5, 10/9 | 22.404 | 28.0 |
| 7/5, 10/7 | 22.512 | 28.1 |
| 15/11, 22/15 | 23.049 | 28.8 |
| 13/10, 20/13 | 25.786 | 32.2 |
| 7/6, 12/7 | 26.871 | 33.6 |
| 11/9, 18/11 | 27.408 | 34.3 |
| 13/11, 22/13 | 30.790 | 38.5 |
| 13/7, 14/13 | 31.702 | 39.6 |
| 15/8, 16/15 | 31.731 | 39.7 |
| 9/7, 14/9 | 35.084 | 43.9 |
| 9/8, 16/9 | 36.090 | 45.1 |
| 15/14, 28/15 | 39.443 | 49.3 |
| 13/8, 16/13 | 39.472 | 49.3 |
| 音程と補音程 | 誤差 (絶対, ¢) | 誤差 (相対, %) |
|---|---|---|
| 1/1, 2/1 | 0.000 | 0.0 |
| 13/9, 18/13 | 3.382 | 4.2 |
| 5/3, 6/5 | 4.359 | 5.4 |
| 11/10, 20/11 | 5.004 | 6.3 |
| 15/13, 26/15 | 7.741 | 9.7 |
| 11/8, 16/11 | 8.682 | 10.9 |
| 7/4, 8/7 | 8.826 | 11.0 |
| 11/6, 12/11 | 9.363 | 11.7 |
| 5/4, 8/5 | 13.686 | 17.1 |
| 11/7, 14/11 | 17.508 | 21.9 |
| 3/2, 4/3 | 18.045 | 22.6 |
| 13/12, 24/13 | 21.427 | 26.8 |
| 9/5, 10/9 | 22.404 | 28.0 |
| 7/5, 10/7 | 22.512 | 28.1 |
| 15/11, 22/15 | 23.049 | 28.8 |
| 13/10, 20/13 | 25.786 | 32.2 |
| 7/6, 12/7 | 26.871 | 33.6 |
| 11/9, 18/11 | 27.408 | 34.3 |
| 13/11, 22/13 | 30.790 | 38.5 |
| 15/8, 16/15 | 31.731 | 39.7 |
| 9/8, 16/9 | 36.090 | 45.1 |
| 13/8, 16/13 | 39.472 | 49.3 |
| 15/14, 28/15 | 40.557 | 50.7 |
| 9/7, 14/9 | 44.916 | 56.1 |
| 13/7, 14/13 | 48.298 | 60.4 |
15平均律の音程と近似値
各周波数比の大きさが16以内で表現される純正音程は以下のようになる。これはedjirulerを用いて、[number of equal divisions=15, interval of equivalence=2, integer limit=16, threshold of JI pitch inclusion=0.25]というパラメータで生成したものである。「The “neighborhood” of JI」の一覧はこちら(huygens-fokker)を参照のこと。
| EDO | interval | cent | DMS | The "neighborhood" of JI | Japanese name | ratio | diff cent | cent | diff DMS | DMS |
| 15 | 0 | 0.00 | 0.00 | |||||||
| 1 | 80.00 | 24.00 | ||||||||
| 2 | 160.00 | 48.00 | 3/4-tone, undecimal neutral second | 3/4全音、11リミットの中立的な2度 | 12/11 | 9.36 | 150.64 | 2.81 | 45.19 | |
| 2 | 160.00 | 48.00 | 4/5-tone, Ptolemy's second | 4/5全音、プトレマイオスの2度 | 11/10 | -5.00 | 165.00 | -1.50 | 49.50 | |
| 3 | 240.00 | 72.00 | septimal whole tone | 7リミットの全音 | 8/7 | 8.83 | 231.17 | 2.65 | 69.35 | |
| 3 | 240.00 | 72.00 | tridecimal 5/4-tone | 13リミットの5/4全音 | 15/13 | -7.74 | 247.74 | -2.32 | 74.32 | |
| 4 | 320.00 | 96.00 | minor third | 短3度 | 6/5 | 4.36 | 315.64 | 1.31 | 94.69 | |
| 5 | 400.00 | 120.00 | major third | 長3度 | 5/4 | 13.69 | 386.31 | 4.11 | 115.89 | |
| 5 | 400.00 | 120.00 | undecimal diminished fourth or major third | 11リミットの減4度または長3度 | 14/11 | -17.51 | 417.51 | -5.25 | 125.25 | |
| 6 | 480.00 | 144.00 | perfect fourth | 完全4度 | 4/3 | -18.04 | 498.04 | -5.41 | 149.41 | |
| 7 | 560.00 | 168.00 | undecimal semi-augmented fourth | 11リミットの準増5度 | 11/8 | 8.68 | 551.32 | 2.60 | 165.40 | |
| 8 | 640.00 | 192.00 | tridecimal diminished fifth | 13リミットの減5度 | 13/9 | 3.38 | 636.62 | 1.01 | 190.99 | |
| 8 | 640.00 | 192.00 | undecimal semi-diminished fifth | 11リミットの準減5度 | 16/11 | -8.68 | 648.68 | -2.60 | 194.60 | |
| 9 | 720.00 | 216.00 | perfect fifth | 完全5度 | 3/2 | 18.04 | 701.96 | 5.41 | 210.59 | |
| 10 | 800.00 | 240.00 | undecimal augmented fifth | 11リミットの増5度 | 11/7 | 17.51 | 782.49 | 5.25 | 234.75 | |
| 10 | 800.00 | 240.00 | minor sixth | 短6度 | 8/5 | -13.69 | 813.69 | -4.11 | 244.11 | |
| 11 | 880.00 | 264.00 | major sixth, BP sixth | 長6度、ボーレン・ピアスの6度 | 5/3 | -4.36 | 884.36 | -1.31 | 265.31 | |
| 12 | 960.00 | 288.00 | harmonic seventh | 協和する7度 | 7/4 | -8.83 | 968.83 | -2.65 | 290.65 | |
| 13 | 1040.00 | 312.00 | 21/4-tone, undecimal neutral seventh | 21/4全音、11リミットの中立7度 | 11/6 | -9.36 | 1049.36 | -2.81 | 314.81 | |
| 14 | 1120.00 | 336.00 | ||||||||
| 15 | 1200.00 | 360.00 |
イメージ
15edo wheel.png15edo wheel 02.png15edo wheel 03.png
12平均律の音程と近似値
15平均律は6/5や5/3といった周波数比5の中で、12平均律以上にいくつかの小さな改善点を提案する。そしてよりよい7倍音や11倍音の響きの近似を持つ。しかし3倍音からは離れる。この近似から抜け出すための特別な方法を行うと、バグと同様にたくさんの特徴をもつ、5L5sMOS音階を構築する。5L5sMOS音階の各音は7リミットオトーナルとウトーナルテトラのためのルートとして役立つ。同様に5リミットのメジャーまたはマイナーセブンスコードとしても役立つ。ウトーナルとはいくつかの周波数の最大公倍数のリミットを差し、オトーナルとは最大値をさす。たとえば10:12:15のコードは5リミットのウトーナリティであり、15リミットのオトーナリティである(otonality and utonality)。5L5sMOS音階はBlackwood temperamentとして知らており、Easley Blackwood, Jrから名づけられている。彼は初めてこれを文章で残した。この文章はまた、Igliashon Jonesにより、「Five is Not an Odd Number」で広範囲にわたり書かれている。15平均律の深いハーモニーの扱い方は、基本的にこのテンペラメントと7と11リミットの拡張にもとづく。Harmony in 15edo Blacksmith[10]もまた参照のこと。
記譜法
15平均律の記譜法にはさまざまな方法がある。そして記譜法の選択は、作曲家が重点を置く点が、ランク2テンペラメントなのか、MOS音階なのかに大きく依存している。
Blackwoodの記譜法
10進数バージョン:1から0(0は10という意味)という言葉を使い、5平均律の3つのチェーンの1つは奇数によってあらわされる。偶数によって2番目が表される。そして3番目は臨時記号のついた数で表される。3番目の臨時記号は奇数にシャープをつけたものでも、偶数にフラットをつけたものでも構わない。
ギターバージョン:15平均律ギターにおいて、5平均律からうまれる「完全4度」のため、すべての開放弦は完全4度でチューニングすることが可能である。そして間隔は正確に2オクターブのままである。もしBから4度圏を始めるなら(B-E-A-D-G-(B))、その時開放弦は通常(E-A-D-G-B-E)として記録される。しかしながら、4度圏は5回で閉じてしまう。15平均律の残り10音に続かないのである。臨時記号を用いて5平均律の2つのチェーンを記録する必要がある。この記譜法は5平均律ではない、臨時記号を使う5線譜にもとづくものとしても、特別なものではない。しかしながらギターにおける15平均律の直感的アプローチが反映されているため、便利である。なぜなら5平均律は、フレットボードをナビゲートするのに便利な3リミットのランドマーク(完全4度や完全5度)のセットという利便性を提供するためである。コードチャートを書くのに特に便利で、そこでは独創的な臨時記号を表す記号は無視できる。
ポーキュパイン・ノーテーション
MOS音階の一種。porcupine notationを参照のこと。
ランク2テンペラメント
| Periods
per octave |
Generator | Temperaments |
|---|---|---|
| 1 | 1\15 | Nautilus/valentine |
| 1 | 2\15 | Porcupine/opossum |
| 1 | 4\15 | Hanson/keemun/orgone |
| 1 | 7\15 | Progress |
| 3 | 1\15 | Augmented/augene |
| 3 | 2\15 | Triforce |
| 5 | 1\15 | Blackwood/blacksmith |
コンマをなだらかにする
15平均律のヴァルを ⟨15 24 35 42 52 56] とみなした時、次のリストのコンマをテンパーアウトする。
| Comma | Monzo | Value (Cents) | Name 1 | Name 2 | Name 3 |
|---|---|---|---|---|---|
| 256/243 | | 8 -5 > | 90.22 | Limma | Pythagorean Minor 2nd | |
| 250/243 | | 1 -5 3 > | 49.17 | Maximal Diesis | Porcupine Comma | |
| 128/125 | | 7 0 -3 > | 41.06 | Diesis | Augmented Comma | |
| 15625/15552 | | -6 -5 6 > | 8.11 | Kleisma | Semicomma Majeur | |
| 1029/1000 | | -3 1 -3 3 > | 49.49 | Keega | ||
| 49/48 | | -4 -1 0 2 > | 35.70 | Slendro Diesis | ||
| 64/63 | | 6 -2 0 -1 > | 27.26 | Septimal Comma | Archytas' Comma | Leipziger Komma |
| 64827/64000 | | -9 3 -3 4 > | 22.23 | Squalentine | ||
| 875/864 | | -5 -3 3 1 > | 21.90 | Keema | ||
| 126/125 | | 1 2 -3 1 > | 13.79 | Septimal Semicomma | Starling Comma | |
| 4000/3969 | | 5 -4 3 -2 > | 13.47 | Octagar | ||
| 1029/1024 | | -10 1 0 3 > | 8.43 | Gamelisma | ||
| 6144/6125 | | 11 1 -3 -2 > | 5.36 | Porwell | ||
| 250047/250000 | | -4 6 -6 3 > | 0.33 | Landscape Comma | ||
| 100/99 | | 2 -2 2 0 -1 > | 17.40 | Ptolemisma | ||
| 121/120 | | -3 -1 -1 0 2 > | 14.37 | Biyatisma | ||
| 176/175 | | 4 0 -2 -1 1 > | 9.86 | Valinorsma | ||
| 65536/65219 | | 16 0 0 -2 -3 > | 8.39 | Orgonisma | ||
| 385/384 | | -7 -1 1 1 1 > | 4.50 | Keenanisma | ||
| 441/440 | | -3 2 -1 2 -1 > | 3.93 | Werckisma | ||
| 4000/3993 | | 5 -1 3 0 -3 > | 3.03 | Wizardharry | ||
| 3025/3024 | | -4 -3 2 -1 2 > | 0.57 | Lehmerisma | ||
| 91/90 | | -1 -2 -1 1 0 1 > | 19.13 | Superleap | ||
| 676/675 | | 2 -3 -2 0 0 2 > | 2.56 | Parizeksma |
理論
The 15-Tone Scale System by Ivor Darreg Permalink
15-EDO Tutorial by Brent Carson Permalink
実践理論と本
Sword, Ronald. "Pendecaphonic Scales for Guitar" IAAA Press, UK-USA. First Ed: June 2009. 15平均律において知られている、すべての音階とテンペラメントファミリーのレポジトリ。300以上の例とコード進行がおさめられている。