19平均律

提供: Xenharmonic Wiki
（19edoから転送）
ナビゲーションに移動 検索に移動
← 18平均律19平均律20平均律 →
素因数分解 19（素数）
音程 63.1579¢ 
完全五度 11\19 (694.737¢)
半音比 (A1:m2) 1:2 (63.16¢ : 126.3¢)
一貫限度 9
厳密一貫限度 5
特異性
フリー百科事典ウィキペディアに以下の記事があります:

19平均律、または 19音平均律（英: 19 equal divisions of the octave, 19 equal temperament, 19EDO, 19ET）は、レギュラー音律の観点から見ると、オクターブを均等な 19個のステップに分割した調律システムである。

それぞれのステップの周波数比は2の19乗根 [math]2^{1/19}[/math] であり、約 63.158 ¢ である。

理論

歴史

この調律システムへの関心は16世紀、作曲家のGuillaume Costeleyが1558年に自身のシャンソン「Seigneur Dieu ta pitié (en) 」に使用した頃にさかのぼる。Costeleyはこの調律のサーキュレート的な性質を理解し、また欲しており、彼はこの調律を、純正長2度を3つのほぼ等しい間隔に分割するものと定義した。Costeleyは減3度などの音程を活用した作品も作った。減3度は19平均律としては意味を持つが、当時の他の調律システムでは意味のないものである。

1577年、音楽理論家のFrancisco de Salinasは、1/3コンマミーントーンを提案した。その5度の大きさは約 694.786 ¢ である。19平均律の5度は約 694.737 ¢ であり、これは約 1/12 ¢ 程度低いだけに過ぎない。Salinasはオクターブをこの方法で19音に調律することを提案したが、19平均律と比べて 1 ¢ にも満たない差しかないので、彼の提案は実質19平均律であった。

1835年、数学者であり音楽理論家のWesley Woolhouseは、彼自身がより良いミーントーン調律だと考えている50平均律 (en) などの、より実用的な代替手段としてこの音律を提案した（Woolhouseのエッセイの要約。）

他の音律への近似として

19平均律の最も顕著な特徴は、ほとんど純正な短3度と、約 7 ¢ 狭い完全5度・長3度を持っているため、ミーントーン音律に適した調律として機能する所である。また、長3度5つの音程が「12度」（ = 完全5度 + 1オクターブ）1つに等しいので、マジック/マグルズ (en) 音律にも適している。

しかし、これら全てに対して、より適した調律が存在する。例えば、19平均律の5度はミーントーンの通常の5度よりも低く、より正確な近似としては31平均律がある。同様に、マジック音律のジェネレーターは長3度であるが、これも19平均律では低く、41平均律 (en) がより正確に合う。マグルズ音律には適した調律になるが、19平均律の場合はマジックと同じとなる。また、19平均律7ステップの上長3度はsensi (en) に使うことができ、sensiのジェネレーターはかなり高い長3度で2つで長6度(5/3 (en) )に近似するのだが、sensiの13リミット (en) 近似には27平均律 (en) や46平均律 (en) の方がより適している。

ただ、これら全てにおいて、19平均律には必要なピッチがより少なくて済むという実践的な利点があり、その結果物理的な実現がより簡単になる（実際、たくさんの19平均律楽器が制作されてきている。）

19平均律は、12平均律に次いで二番目の、5リミット (en) 音楽を許容出来る方法で扱うことのできる平均律であり、また、12平均律に次いで五番目のゼータ積分平均律 (en) である。7倍音系短三度(7/6 (en) )と7倍音系全音(8/7 (en) )の間の区別がなくなってしまうので、19平均律は7リミットではあまり上手くいかない（しかし12平均律よりは良い。）

19平均律はnegri (en) 、keemun (en) 、ゴジラ (en) 、マジック/マグルズ、トリトン (en) /liese (en) などに最適であり、さらにsensiにもかなり適しているという利点を有している。keemunやnegriはとてもシンプルな7リミット音律であるという点で注目に値し、19平均律におけるMOSスケールは非常に豊富な7倍音系四和音を提供する。7リミット四和音のGraham複雑度 (en) はkeemunでは6、negriでは7、ゴジラでは8、ミーントーンでは10、トリトンでは11、マジック/マグルズでは12、そしてsensiでは13である。

ゼータ積分調律なので、13リミットは比較的よく表現されているが、一貫性がある表現がされているのは 2.3.5.7.13 サブグループのみである。実際には、19平均律は音を上にベンドできる楽器に適応的に使用できる。大きさは様々だが、3, 5, 7, および13倍音はすべて低くチューニングされる。同じことは12平均律では言えず、12平均律では5, 7倍音が19平均律のときよりも純正から遠くなるだけでなく、かなり高くなる。19平均律のnegri、sensi、セマフォ (en) スケールには13リミットのコードが多く含まれている。（通常のディミニッシュスケールに対する19平均律の対応物としてsensi[8] 3L 5s (en) MOSスケールを思い浮かべてみよ。どちらも2つのディミニッシュセブンスコードで構成されているが、sensi[8] では7と13倍音の追加の比率が得られる。）

別の手段は、伸長されたオクターブを使用することだ。ゼータ関数的に最適な調律のオクターブは約 1203 ¢ である。弦楽器、特にピアノは、弦に固有のインハーモニシティのため、オクターブを伸ばして調律されることが多いため、19平均律はそれらにとって有望な選択肢となる。オクターブ伸長は、チューニングがずれている音程を、ほぼ正確に調整した、複合したあるいは反転した音程に置き換えることができることも意味する。たとえば、93ED30 (en) （30/1が純正である19平均律の変形）を使用すれば、ほぼ純正な短3度(6/5)、複合長3度(5/1)、および複合5度(6/1)が得られ、5リミット調性ダイヤモンド内のすべての比が提供される。複合メジャー三和音とマイナー三和音(1:5:6 および 30:6:5)も同様にほぼ純正となる。

ハーモニーを拡張する手段として

19平均律は12平均律よりも多くの調和した協和ハーモニーを実現できるため、4度堆積、2度堆積、ポリコードなどの代替のハーモニーを使用する場合に適している。William Lynch (en) は、不完全とみなされている三和音とともに、さまざまな種類のセブンスコードを基本的な響きとして扱うことを提案している。12平均律では衝突する傾向がある、7倍音や他の非ダイアトニックコード的拡張を含む、より高次倍音への拡張は、19平均律ではより良く調和する。

さらに、Joseph Yasser (en) は、その内の7音メジャースケールが西洋音楽のペンタトニックに似たものになる、19平均律の12音スプラダイアトニックスケールのアイデアについて話している。将来の世代には曖昧で、トーンに活力がないように聴こえるかもしれない[訳不正確]。言い換えれば、「音の重力という否定できない法則が存在するシステムでありながら、はるかに複雑な音の世界」である。Yasserは、音楽は最終的には12音スプラダイアトニックスケールを備えた19音システムに移行し、標準になるだろうと信じていた。これはまだ実現していないが、Yasserのスプラダイアトニック性の概念は興味深いものであり、異質に聴こえすぎずに調性を拡張したい人にとっては検討する価値がある。

19平均律はまた、Bozuji調律 (en) （Gioseffo Zarlinoの純正律へのアプローチに基づいた21世紀のチューニング）の音程のほとんどに非常に近似している。Bozujiチューニングの隣接するダイアトニックの減音程と増音程のほとんどは、19平均律の1つの音程で異名同音的に表される。

19平均律の狭い全音と広いダイアトニック半音は、ダイアトニックスケールにやや鈍い性質を与えるが、ペンタトニックスケールには逆の効果があり、狭い全音と広い短3度の間のコントラストが大きくなるため、より表現力豊かになる。12平均律には表現力豊かなダイアトニックと鈍いペンタトニックがあるが、19平均律ではその逆が当てはまる。したがって、19平均律ではペンタトニック中心主義(pentatonicism)がより重要になり、ペンタトニックスケールを一種の「スーパーコード」として使用し、「コード進行」をスーパーダイアトニックスケールのペンタトニック部分セット間の転調とするのが1つの選択となる。

素数倍音

19EDOにおける素数倍音の近似
倍音 2 3 5 7 11 13 17 19 23 29 31
誤差 絶対 (¢) +0.0 -7.2 -7.4 -21.5 +17.1 -19.5 +21.4 +18.3 +3.3 -19.1 -8.2
相対 (%) +0.0 -11.4 -11.7 -34.0 +27.1 -30.8 +33.8 +28.9 +5.2 -30.2 -13.0
ステップ
(reduced) 		19
(0) 		30
(11) 		44
(6) 		53
(15) 		66
(9) 		70
(13) 		78
(2) 		81
(5) 		86
(10) 		92
(16) 		94
(18)

部分集合と上位集合

19平均律は8番目の素数平均律 (en) で、1つ前は17平均律、1つ後は23平均律である。

19平均律を2倍にした38平均律は、5リミットマッピングのフラットな傾向とうまく機能する11倍音の近似を提供する。詳しくはundevigintone (en) を参照。57平均律は7倍音を効果的に純正に補正するが、最もよく適合するのは76平均律である。詳しくはmeanmag (en) を参照。

19平均律の音程と近似値

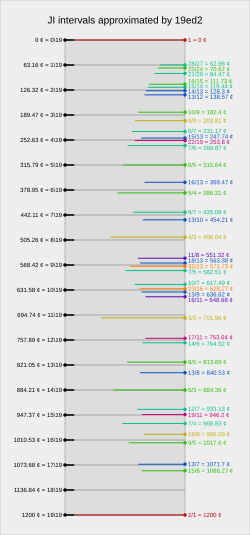
19平均律で表現できる、各周波数比の分母分子が16以下の純正音程は以下のようになる。これはedjirulerを用いて、[number of equal divisions=19, interval of equivalence=2, integer limit=16, threshold of JI pitch inclusion=0.3]というパラメータで生成したものである。純正音程名の一覧はこちら（huygens-fokker）を参照のこと。

平均律 音程 セント DMS 「近所」のJI 日本語名 比率 誤差(¢) セント 誤差(DMS) DMS
19 0 0.00 0.00
1 63.16 18.95 classic chromatic semitone 古典的クロマティック半音 25/24 -7.51 70.67
2 126.32 37.89 classic diatonic semitone 古典的ダイアトニック半音 16/15 14.58 111.73 4.38 33.52
2 126.32 37.89 septimal diatonic semitone 7倍音系ダイアトニック半音 15/14 6.87 119.44 2.06 35.83
2 126.32 37.89 tridecimal 2/3-tone 13倍音系2/3-音 14/13 -1.98 128.30 -0.59 38.49
2 126.32 37.89 tridecimal neutral second 13倍音系中2度 13/12 -12.26 138.57 -3.68 41.57
3 189.47 56.84 small whole tone 小全音 10/9 7.07 182.40 2.12 54.72
3 189.47 56.84 Pythagorean whole tone 大全音
ピタゴラスの全音 		9/8 -14.44 203.91 -4.33 61.17
4 252.63 75.79 tridecimal 5/4-tone 13倍音系5/4-音 15/13 4.89 247.74 1.47 74.32
4 252.63 75.79 septimal minor third
subminor third 		7倍音系短3度
下短3度
縮3度 		7/6 -14.24 266.87 -4.27 80.06
5 315.79 94.74 minor third 短3度 6/5 0.15 315.64 0.04 94.69
6 378.95 113.68 major third 長3度 5/4 -7.37 386.31 -2.21 115.89
7 442.11 132.63 septimal major third
supermajor third
BP third 		7倍音系長3度
上長3度
拡3度
ボーレン・ピアースの3度 		9/7 7.02 435.08 2.11 130.53
7 442.11 132.63 tridecimal semisixth 13倍音系半6度 13/10 -12.11 454.21 -3.63 136.26
8 505.26 151.58 perfect fourth 完全4度 4/3 7.22 498.04 2.17 149.41
9 568.42 170.53 undecimal superfourth 11倍音系上4度(拡4度) 11/8 17.10 551.32 5.13 165.40
9 568.42 170.53 Huygens' tritone
BP fourth 		ホイヘンスの3全音
ボーレン・ピアースの4度 		7/5 -14.09 582.51 -4.23 174.75
10 631.58 189.47 Euler's tritone オイラーの3全音 10/7 14.09 617.49 4.23 185.25
10 631.58 189.47 tridecimal diminished fifth 13倍音系減5度 13/9 -5.04 636.62 -1.51 190.99
10 631.58 189.47 undecimal subfifth 11倍音系下5度(縮5度) 16/11 -17.10 648.68 -5.13 194.60
11 694.74 208.42 perfect fifth 完全5度 3/2 -7.22 701.96 -2.17 210.59
12 757.89 227.37 septimal minor sixth
subminor sixth 		7倍音系短6度
下短6度
縮6度 		14/9 -7.02 764.92 -2.11 229.47
13 821.05 246.32 minor sixth 短6度 8/5 7.37 813.69 2.21 244.11
14 884.21 265.26 major sixth
BP sixth 		長6度
ボーレン・ピアースの6度 		5/3 -0.15 884.36 -0.04 265.31
15 947.37 284.21 septimal major sixth
supermajor sixth 		7倍音系長6度
上長6度
拡6度 		12/7 14.24 933.13 4.27 279.94
16 1010.53 303.16 Pythagorean minor seventh ピタゴラスの短7度 16/9 14.44 996.09 4.33 298.83
16 1010.53 303.16 classic minor seventh
BP seventh 		古典的短7度
ボーレン・ピアースの7度 		9/5 -7.07 1017.60 -2.12 305.28
17 1073.68 322.11 16/3-tone 16/3-音 13/7 1.98 1071.70 0.59 321.51
17 1073.68 322.11 classic major seventh 古典的長7度 15/8 -14.58 1088.27 -4.38 326.48
18 1136.84 341.05 classic diminished octave 古典的減オクターヴ 48/25 7.51 1129.33
19 1200.00 360.00

音程

五線譜や文字記譜(標準の臨時記号付き)、ソルフェージュ、sargamなどいずれにおいても、標準の12平均律の記譜法を使用できる。D#とEbは2つの異なる音であることに注意。

# セント 近似周波数比[1] 音程 ソルフェージュ (en) ドデカトニック表記
0 0.00 1/1 完全1度, ユニゾン P1 C ド(Do) P1
1 63.16 25/24, 28/27, 26/25 増1度, 減2度 A1, d2 C#, Dbb ディ(Di)
ロ(Ro) 		A1, m2
2 126.32 15/14, 16/15, 13/12, 14/13 短2度 m2 Db ラ(Ra) M2, m3
3 189.47 9/8, 10/9, 125/112 長2度 M2 D レ(Re) M3
4 252.63 7/6, 8/7, 15/13 増2度, 減3度 A2, d3 D#, Ebb リ(Ri)
マ(Ma) 		m4, a3
5 315.79 6/5 短3度 m3 Eb メ(Me) M4, m5
6 378.95 5/4, 16/13, 56/45 長3度 M3 E ミ(Mi) M5
7 442.11 32/25, 9/7, 13/10 増3度, 減4度 A3, d4 E#, Fb モ(Mo)
フェ(Fe) 		A5, d6
8 505.26 4/3, 75/56 完全4度 P4 F ファ(Fa) P6
9 568.42 25/18, 7/5, 18/13 増4度 A4 F# フィ(Fi) A6, m7
10 631.58 36/25, 10/7, 13/9 減5度 d5 Gb セ(Se) M7, d8
11 694.74 3/2, 112/75 完全5度 P5 G ソ(So) P8
12 757.89 25/16, 14/9, 20/13 増5度, 減6度 A5, d6 G#, Abb スィ(Si)
ロ(Lo) 		A8, m9
13 821.05 8/5, 13/8, 45/28 短6度 m6 Ab レ(Le) M9, m10
14 884.21 5/3 長6度 M6 A ラ(La) M10
15 947.37 7/4, 12/7, 26/15 増6度, 減7度 A6, d7 A#, Bbb リ(Li)
タ(Ta) 		m11, A10
16 1010.53 9/5, 16/9, 224/125 短7度 m7 Bb テ(Te) M11, m12
17 1073.68 15/8, 13/7, 28/15, 24/13 長7度 M7 B ティ(Ti) M12
18 1136.84 48/25, 27/14, 25/13 増7度, 減8度 A7, d8 B#, Cb ト(To)
ダ(Da) 		A12, d13
19 1200.00 2/1 完全8度, オクターブ P8 C ド(Do) P13
  1. ↑ 19平均律を2.3.5.7.13サブグループ音律として扱った場合に基づく。他のアプローチも可能である。

カラー表記においての音程の詳細度数とコードの名前

カラー表記を使用すると、クオリティをカラーと大まかに関連付けることができる。

クオリティ カラーネーム (en) モンゾ表記 例
ディミニッシュ zo [a b 0 1⟩ 7/6, 7/4
マイナー fourthward wa [a b⟩ (b < -1) 32/27, 16/9
gu [a b -1⟩ 6/5, 9/5
メジャー yo [a b 1⟩ 5/4, 5/3
fifthward wa [a b⟩ (b > 1) 9/8, 27/16
オーギュメント ru [a b 0 -1⟩ 9/7, 12/7

調号は同じだが、追加の音符や異なる異名同音により、一部の調号が乱雑になることがある。例えば、B𝄫キーでは、BとEにダブルフラットが付き、C, D, F, G, Aにフラットが付く。これをA♯に書き換えると良いように思われるかもしれないが、その場合、C, F, Gにダブルシャープが付き、A, B, D, Eにシャープが付くことになり、実際にはより悪くなる。

すべての19平均律のコードは従来の方法を使用して名前を付けることができ、増/減2度、3度、6度、および7度を含むように拡張できる。zo, gu, yo, ruのトライアドは次のとおりである。

3度のカラー (en) 純正コード ステップ数 Cコードでの表記 書き方 読み方
zo 6:7:9 0–4–11 C–E𝄫–G Csm, C(♭3), C(d3) Cサブマイナー, Cフラットスリー, Cディミニッシュスリー
gu 10:12:15 0–5–11 C–E♭–G Cm Cマイナー
yo 4:5:6 0–6–11 C–E–G C Cメジャー, C
ru 14:18:21 0–7–11 C–E♯–G CSM, C(♯3), C(A3) Cスーパーメジャー, Cシャープスリー, Cオーギュメントスリー
– 4:5:6:7 0–6–11–15 C–E–G–B𝄫 C(h7), Cadd(d7), CM(d7) Cアドディミニッシュセブン, Cメジャーディミニッシュセブン
– 70:84:105:120 = 1/(4:5:6:7) 0–5–11–15 C–E♭–G–A♯ Cm(♯6), Cm(A6) Cマイナーシャープシックス, Cマイナーオーギュメントシックス

最後の2つのコードは、15\19 の音程が 7/4 または 12/7 のいずれかであるとどのようにみなされうるか、および19平均律がどのようにzoとruの比率を混同しうるかを示している。

より完全なリストについては、19平均律のコードネーム (en) とアップ & ダウン表記 #コードとコード進行 (en) を参照。

純正音程への近似

純正音程のマッピング

以下の表は、19平均律で15奇数リミット音程がどのように表されるかを示している。素数倍音は太字で、非一貫的な音程は斜体で示す。

19平均律内の15奇数リミット音程（直接近似, 一貫性の無いものも含む）
音程と補音程 誤差 (絶対, ¢) 誤差 (相対, %)
1/1, 2/1 0.000 0.0
5/3, 6/5 0.148 0.2
13/7, 14/13 1.982 3.1
15/13, 26/15 4.891 7.7
13/9, 18/13 5.039 8.0
15/14, 28/15 6.873 10.9
9/7, 14/9 7.021 11.1
9/5, 10/9 7.070 11.2
3/2, 4/3 7.218 11.4
5/4, 8/5 7.366 11.7
13/10, 20/13 12.109 19.2
13/12, 24/13 12.257 19.4
7/5, 10/7 14.091 22.3
7/6, 12/7 14.239 22.5
9/8, 16/9 14.436 22.9
15/8, 16/15 14.585 23.1
11/8, 16/11 17.103 27.1
13/8, 16/13 19.475 30.8
7/4, 8/7 21.457 34.0
11/6, 12/11 24.321 38.5
11/10, 20/11 24.469 38.7
11/7, 14/11 24.597 38.9
13/11, 22/13 26.580 42.1
15/11, 22/15 31.470 49.8
11/9, 18/11 31.539 49.9
19平均律内の15奇数リミット音程（パテントヴァルによるマッピング）
音程と補音程 誤差 (絶対, ¢) 誤差 (相対, %)
1/1, 2/1 0.000 0.0
5/3, 6/5 0.148 0.2
13/7, 14/13 1.982 3.1
15/13, 26/15 4.891 7.7
13/9, 18/13 5.039 8.0
15/14, 28/15 6.873 10.9
9/7, 14/9 7.021 11.1
9/5, 10/9 7.070 11.2
3/2, 4/3 7.218 11.4
5/4, 8/5 7.366 11.7
13/10, 20/13 12.109 19.2
13/12, 24/13 12.257 19.4
7/5, 10/7 14.091 22.3
7/6, 12/7 14.239 22.5
9/8, 16/9 14.436 22.9
15/8, 16/15 14.585 23.1
11/8, 16/11 17.103 27.1
13/8, 16/13 19.475 30.8
7/4, 8/7 21.457 34.0
11/6, 12/11 24.321 38.5
11/10, 20/11 24.469 38.7
11/9, 18/11 31.539 49.9
15/11, 22/15 31.688 50.2
13/11, 22/13 36.578 57.9
11/7, 14/11 38.561 61.1
alt : お使いのブラウザはSVG形式に対応しておりません。
19平均律で近似されるいくつかの19-リミット音程

レギュラー音律の性質

サブグループ コンマリスト (en) マッピング (en) 最適なオクターヴ伸縮幅 (¢) 誤差
絶対 (¢) 相対 (%)
2.3 [-30 19⟩ [⟨19 30]] +2.28 2.28 3.61
2.3.5 81/80, 3125/3072 [⟨19 30 44]] +2.58 1.91 3.02
2.3.5.7 49/48, 81/80, 126/125 [⟨19 30 44 53]] +3.85 2.76 4.35
2.3.5.7.13 49/48, 65/64, 81/80, 91/90 [⟨19 30 44 53 70]] +4.14 2.53 3.99

19平均律は、5, 7, 13, 17, 19リミットにおいて、これまでのどの平均律よりも相対誤差が低くなる。13リミットでは19と19eの両方のヴァルが、17リミットでは19egのヴァルが、そして19リミットでは19eghのヴァルがこれを達成する。これらのサブグループでより優れている次の平均律は、それぞれ34, 31, 27e, 22, および26である。

19平均律は2.3.5.7.13サブグループで卓越しており、このサブグループでより優れている次の平均律は53である。

一様写像

18.5と19.5の間の13リミット一様写像
最小サイズ 最大サイズ Wart記法 Map
18.5000 18.5113 19bbccddeeeffff ⟨19 29 43 52 64 68]
18.5113 18.6124 19bbccddeeeff ⟨19 29 43 52 64 69]
18.6124 18.6447 19ccddeeeff ⟨19 30 43 52 64 69]
18.6447 18.7009 19ccddeff ⟨19 30 43 52 65 69]
18.7009 18.7344 19cceff ⟨19 30 43 53 65 69]
18.7344 18.7816 19eff ⟨19 30 44 53 65 69]
18.7816 18.9337 19e ⟨19 30 44 53 65 70]
18.9337 19.0518 19 ⟨19 30 44 53 66 70]
19.0518 19.0571 19f ⟨19 30 44 53 66 71]
19.0571 19.1651 19df ⟨19 30 44 54 66 71]
19.1651 19.2228 19cdf ⟨19 30 45 54 66 71]
19.2228 19.2434 19cdeef ⟨19 30 45 54 67 71]
19.2434 19.3220 19bcdeef ⟨19 31 45 54 67 71]
19.3220 19.4133 19bcdeefff ⟨19 31 45 54 67 72]
19.4133 19.5000 19bcdddeefff ⟨19 31 45 55 67 72]

コンマ

ヴァルを ⟨19 30 44 53 66 70] としたとき、19平均律は次のコンマをテンパーアウトする。

素数リミット (en) 比率[1] モンゾ セント カラーネーム (en) 名前
3 (20 digits) [-30 19⟩ 137.14
5 16875/16384 [-14 3 4⟩ 51.12 Laquadyo Negri comma
5 3125/3072 [-10 -1 5⟩ 29.61 Laquinyo Magic comma
5 81/80 [-4 4 -1⟩ 21.51 Gu Syntonic comma
5 78732/78125 [2 9 -7⟩ 13.40 Sepgu Sensipent comma
5 15625/15552 [-6 -5 6⟩ 8.11 Tribiyo Kleisma
5 (20 digits) [8 14 -13⟩ 5.29 Thegu Parakleisma
5 (28 digits) [-14 -19 19⟩ 2.82 Neyo Enneadeca
7 1029/1000 [-3 1 -3 3⟩ 49.49 Trizogu Keega
7 525/512 [-9 1 2 1⟩ 43.41 Lazoyoyo Avicennma
7 49/48 [-4 -1 0 2⟩ 35.70 Zozo Slendro diesis
7 686/675 [1 -3 -2 3⟩ 27.99 Trizo-agugu Senga
7 875/864 [-5 -3 3 1⟩ 21.90 Zotrigu Keema
7 245/243 [0 -5 1 2⟩ 14.19 Zozoyo Sensamagic
7 126/125 [1 2 -3 1⟩ 13.79 Zotrigu Starling comma
7 225/224 [-5 2 2 -1⟩ 7.71 Ruyoyo Marvel comma
7 19683/19600 [-4 9 -2 -2⟩ 7.32 Labirugu Cataharry
7 10976/10935 [5 -7 -1 3⟩ 6.48 Satrizo-agu Hemimage
7 3136/3125 [6 0 -5 2⟩ 6.08 Zozoquingu Hemimean
7 (12 digits) [-11 2 7 -3⟩ 1.63 Latriru-asepyo en:Meter
7 4375/4374 [-1 -7 4 1⟩ 0.40 Zoquadyo Ragisma
11 100/99 [2 -2 2 0 -1⟩ 17.40 Luyoyo Ptolemisma
11 896/891 [7 -4 0 1 -1⟩ 9.69 Saluzo Pentacircle comma
11 65536/65219 [16 0 0 -2 -3⟩ 8.39 Satrilu-aruru Orgonisma
11 385/384 [-7 -1 1 1 1⟩ 4.50 Lozoyo Keenanisma
11 540/539 [2 3 1 -2 -1⟩ 3.21 Lururuyo Swetisma
13 65/64 [-6 0 1 0 0 1⟩ 26.84 Thoyo Wilsorma
13 343/338 [-1 0 0 3 0 -2⟩ 25.42 Thuthutrizo
13 91/90 [-1 -2 -1 1 0 1⟩ 19.13 Thozogu Superleap
13 676/675 [2 -3 -2 0 0 2⟩ 2.56 Bithogu Island comma
  1. ↑ 10桁を超える比率は、桁数を表記したプレースホルダーによって示される。

線形音律

19は素数であるため、19平均律のランク2の音律はすべて、オクターブごとに1つの周期を持つ（つまり線形）。したがって、音程とそれが生成する線形音律とを対応付けることができる。

度数 セント 音程 MOS 音律
1 63.16 A1, d2 Unicorn / rhinocerus
2 126.32 m2 1L 8s, 9L 1s Negri
3 189.47 M2 1L 5s, 6L 1s, 6L 7s Deutone
Spell
4 252.63 A2, d3 1L 3s, 4L 1s,
5L 4s, 5L 9s 		Godzilla
5 315.79 m3 3L 1s, 4L 3s,
4L 7s, 4L 11s 		Cata / keemun
6 378.95 M3 3L 1s, 3L 4s, 3L 7s,
3L 10s, 3L 13s 		マジック / muggles
7 442.11 A3, d4 3L 2s, 3L 5s, 8L 3s Sensi
8 505.26 P4 2L 3s, 5L 2s, 7L 5s Meantone / flattone
9 568.42 A4 2L 3s, 2L 5s, 2L 7s,
2L 9s, 2L 11s, 2L 13s,
2L 15s 		Liese / pycnic
Triton

スケール

MOSスケール

オクターブ等価MOS

  • ミーントーンペンタトニック, 2L 3s (gen = 11\19): 33535
  • ミーントーンダイアトニック, 5L 2s (gen = 11\19): 3323332
  • ミーントーンクロマティック, 7L 5s (gen = 11\19): 212122121212
  • セマフォ (en) [5], 4L 1s (gen = 4\19): 44344
  • セマフォ[9], 5L 4s (gen = 4\19): 313133131
  • セマフォ[14], 5L 9s (gen = 4\19): 21211211211211
  • sensi (en) [5], 2L 3s (gen = 7\19): 52525
  • sensi[8], 3L 5s (gen = 7\19): 23223223
  • sensi[11], 8L 3s (gen = 7\19): 22122212221
  • Negri (en) [9], 1L 8s (gen = 2\19): 222232222
  • negri[10], 9L 1s (gen = 2\19): 2222212222
  • kleismic (en) [7], 4L 3s (gen = 5\19): 1414144
  • kleismic[11], 4L 7s (gen = 5\19): 13113113131
  • kleismic[15], 4L 11s (gen = 5\19): 121112111211211
  • マジック[7], 3L 4s (gen = 6\19): 5151511
  • マジック[10], 3L 7s (gen = 6\19): 4114114111
  • マジック[13], 3L 10s (gen = 6\19): 3111311131111
  • マジック[16], 3L 13s (gen = 6\19): 2111121111211111
  • liese (en) [17], 2L 15s (gen = 9\19): 2111111111211111111

他のスケール

音楽

en:19edo/Musicも参照のこと。

XA 19-ET Index

日本

楽器

脚注

関連項目

外部リンク

「https://ja.xen.wiki/index.php?title=19平均律&oldid=818」から取得