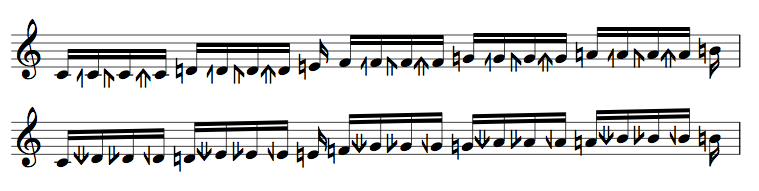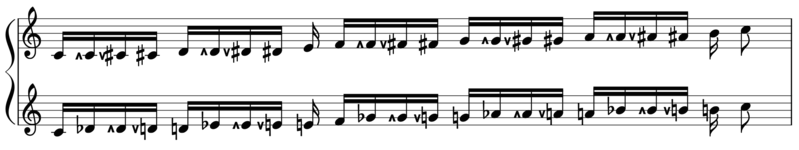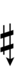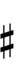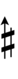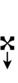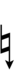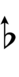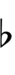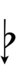利用者:Tessyrrh1016/draft: 22平均律

This page is a draft of JP translation from en:22edo.

素因数分解

2 × 11

音程

54.5455¢

完全五度

13\22 (709.091¢)

半音比 (A1:m2)

3:1 (163.6¢ : 54.55¢)

一貫限度

11

厳密一貫限度

5

特異性

Zeta peak
Zeta peak integer

22平均律、または22音平均律（英: 22 equal divisions of the octave, 22 equal temperament, 22EDO, 22ET）は、レギュラー音律の観点から見ると、オクターブを均等な22個のステップに分割した調律システムである。

1ステップあたりの周波数比は2の22乗根 [math]2^{1/22}[/math] であり、約 54.545 ¢ である。9/8 (en) と 10/9 (en) を区別するので、これはミーントーンシステムではない。

理論

歴史

オクターブを同じサイズの22のステップに分割するという考えは、19世紀の音楽理論家R.H.M. Bosanquetに由来しているようである。インドの音楽理論 (en) におけるオクターブの22の不均等な分割に触発され、Bosanquetは22個への均等な分割により5-リミットの音楽を許容できる精度で表現できることに注目した。この点については、20世紀に理論家のJosé Würschmidtが続き、彼はこれを19平均律の次の可能性として指摘した。また、J. Murray Barbourは、調律の歴史に関する古典的な調査書『Tuning and Temperament』の中で、これに続いた。

純正音程近似のクオリティの概観

22平均律のシステムは、実際には12と19に次ぐ5-リミット (en) 音程をTE誤差 (en) 4 ¢/oct 以内に近似することができる3番目の平均律である。ゼータ積分やゼータギャップ平均律ではないが、少なくともゼータピーク平均律 (en) ではある。さらに12や19とは異なり、5-リミットのみならず、7-リミット (en) 、11-リミット (en) 音程をも 3 ¢/oct 以内の誤差で近似できる。31平均律の方がはるかに優れてはいるものの、22平均律でもこれらの高リミットのハーモニーを利用できる。実際、22は11-奇数リミット (en) を一貫して表す最小の等分割である。

22平均律は12や19とは異なり、ミーントーンシステムではない。22という数字があまり馴染みのない音楽領域の探求を可能にしある程度強制することも効果の一つであるが、最終的な効果はやはり（22という数が小さいので）22音ギターなどの適切に設計された楽器を使用したライブパフォーマンスで使用することが容易いことであろう。

22平均律は、11平均律の 2.7.9.11.15.17 サブグループに倍音3と5を追加したものとして扱うこともでき（かなり正確な）2.3.5.7.11.17 サブグループ音律になる。31倍音の近似値が 0.5 ¢ 以内であり、かなり正確であることも注目に値する。また、特に 29/24 などの29倍音を含むいくつかの間隔も近似しており、これも 0.5 ¢ 以内で一致する。これにより、2.3.5.7.11.17.29.31 がもたらされる。

22平均律は、拡張された「クォーターコンマarchy」に非常に近い。これはテンパーアウトされるコンマがシントニックコンマ(81/80 (en) )である代わりにアルキュタスコンマ(64/63 (en) )であるところ以外は、クォーターコンマミーントーン (en) に似た構造のチューニングである。このため、ほぼ純粋な7倍音系長3度（9/7 (en) ）を持つ。

素数倍音

22EDOにおける素数倍音の近似
倍音		2	3	5	7	11	13	17	19	23	29	31
誤差	絶対 (¢)	+0.0	+7.1	-4.5	+13.0	-5.9	-22.3	+4.1	-24.8	+26.3	+6.8	+0.4
誤差	相対 (%)	+0.0	+13.1	-8.2	+23.8	-10.7	-41.0	+7.6	-45.4	+48.2	+12.4	+0.8
ステップ (reduced)		22 (0)	35 (13)	51 (7)	62 (18)	76 (10)	81 (15)	90 (2)	93 (5)	100 (12)	107 (19)	109 (21)

部分集合と上位集合

22は11で割り切れるため、12平均律が6平均律（全音音階）を演奏できるのと同じように、22平均律楽器は11平均律のあらゆる音楽を演奏できる。11平均律は、旋律的には12平均律（よく知られた 1:2:3 の比率で全音、半音、短3度）に聞こえる点で興味深いが、特に完全5度/4度や5-リミット長3度/短6度がないため、和声的には大きく異なる。同様に、22平均律と24平均律は、どちらも4分音や短/中/長2度を含むため、旋律的に似ている。しかし、22平均律は24よりもはるかに優れた全体的なハーモニーを提供する。

サジタルノーテーション (en) では、11は22の1つおきの音として記譜できる。

音程

en:22edo solfegeも参照のこと。

ステップ	セント	近似音程^[1]	アップ&ダウン表記 (en)
0	0.000	1/1	完全1度, ユニゾン	P1	C
1	54.545	36/35, 34/33, 33/32, 32/31	短2度	m2	D♭
2	109.091	18/17, 17/16, 16/15, 15/14	アップ短2度	^m2	^D♭
3	163.636	12/11, 11/10, 10/9	ダウン長2度	vM2	vD
4	218.182	9/8, 17/15, 8/7	長2度	M2	D
5	272.727	20/17, 7/6	短3度	m3	E♭
6	327.273	6/5, 17/14, 11/9	アップ短3度	^m3	^E♭
7	381.818	5/4, 96/77	ダウン長3度	vM3	vE
8	436.364	14/11, 9/7, 22/17	長3度	M3	E
9	490.909	4/3	完全4度	P4	F
10	545.455	15/11, 11/8	アップ4度, 減5度	^4, d5	^F, G♭
11	600.000	7/5, 24/17, 17/12, 10/7	ダウン増4度, アップ減5度	vA4, ^d5	vF♯, ^G♭
12	654.545	16/11, 22/15	増4度, ダウン5度	A4, v5	F♯, vG
13	709.091	3/2	完全5度	P5	G
14	763.636	17/11, 14/9, 11/7	短6度	m6	A♭
15	818.182	8/5, 77/48	アップ短6度	^m6	^A♭
16	872.727	18/11, 28/17, 5/3	ダウン長6度	vM6	vA
17	927.273	17/10, 12/7	長6度	M6	A
18	981.818	7/4, 30/17, 16/9	短7度	m7	B♭
19	1036.364	9/5, 11/6, 20/11	アップ短7度	^m7	^B♭
20	1090.909	28/15, 15/8, 32/17, 17/9	ダウン長7度	vM7	vB
21	1145.455	31/16, 64/33, 33/17, 35/18	長7度	M7	B
22	1200.000	2/1	完全8度, オクターヴ	P8	C

↑ 22平均律を2.3.5.7.11.17サブグループ音律として扱うことに基づいて、サイズの大きい順に並べられたいくつかの単純な比率。他のアプローチも可能。

記譜法

スーパーパイス/ポーキュパイン記法

スーパーパイス/ポーキュパイン記法は、スーパーパイス音律 (en) とポーキュパイン音律 (en) の両方から生まれた記法である。

まず、5L 2s スーパーパイス[7] による名前を付ける。ただし、不完全音程の前には “s-” をつけ、完全4度・完全5度は「完全」をとって代わりに「本位(natural, 暫定訳語)」を付ける。次に、1L 6s (en) ポーキュパイン[7] による名前を付ける。ただし、各音程の前には “p-” をつける。すると、2, 11, 20ステップ目以外は長、短、本位音程のいずれかにできる。この残った3つはp-減2度、半オクターヴ、p-増7度などと命名できる。

ポーキュパイン記法

ポーキュパイン記法もポーキュパインのジェネレータ(3\22)を使用して記法を作る。2度と7度は完全音程で、4度と5度は3度と6度と同様に不完全音程となる。本位音程は2度の連鎖 A-B-C-D-E-F-G を表す。これは、追加の臨時記号なしで7音階を記譜する唯一の方法である。

キーボードは D * * E * * F * * G * * * A * * B * * C * * D となる。

ペンタトニック記法

ペンタトニック記譜法では、度数はユニゾン・準3度・擬4度・擬5度・準7度・擬8度である。本位音程は5度連鎖 F-C-G-D-A を表す。これは、追加の臨時記号なしで5度連鎖記譜法を使用する唯一の方法である。

要は通常の2L 3s (en) 3|1, マイナーペンタトニックスケール LssLs に12平均律と同様の名前を割り当てたものである。ただしDから始める。

キーボードは D * * * * F * * * G * * * A * * * * C * * * D となる。

デカトニック記法

デカトニック記法は、Paul Erlich (en) の10音音階に基づいている。一般的な記法とは異なり、デカトニックシステムは7音ではなく10音の音階に基づいている。このアプローチでは、コード、音程、記法のすべてをもう一度学習し直す必要があるが、22平均律を1組の臨時記号のみを使用して記譜できるため、7音階的な思考パターンから抜け出す機会が得られる。このシステムは、2つの5度連鎖に基づいている。1つはラテン文字で、もう1つはギリシア文字で表される。2つの連鎖は、2つの並置された5音音階として考えることができる。

連鎖1：C-G-D-A-E

連鎖2：γ-δ-α-ε-β

アルファベットは昇順で、C δ D ε E γ G α A β C となる。

このアルファベットでは、あるラテン文字の組が5度の関係にあるとき、それに対応するギリシャ文字の組も同じく5度の関係になる。たとえば、G-D は5度であるので、γ-δ も5度となる。

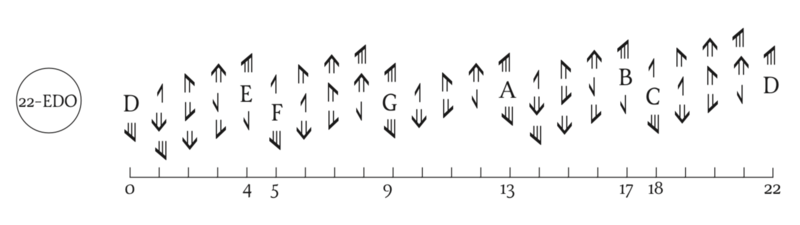
サジタルノーテーション(矢印記法)

22平均律を5度圏によって生成されるものとして扱う場合、本位音 F-C-G-D-A-E-B は 13\22 の反復による5度連鎖を表す。その結果、全音は4ステップになり、アポトメー（apotome, ピタゴラスのシャープ/フラット1つ分の音程）は3ステップになる。アポトメーを3つの部分に分割する3組のサジタル記号のみが必要であり、多くの異名同音が提供される。

この表記は、5-リミット純正音程のサジタルノーテーションと一致している。つまり、「長」3度と6度は、シントニックコンマ1つ分下げられた（スーパー）ピタゴラス音程として現れる。

アポトメーを3つのシントニックコンマに分割するということは、22がポーキュパインコンマ (en) （これは『シントニックコンマ × 3 − アポトメー』と等しい）をテンパーアウトすることを示している。

また、Jacob A. Barton (en) 著のThe Sagittal Songbook (en) の付録には、Revo版（純粋版）サジタル記号で22平均律を表記する方法を示す次の図がある：

アップ&ダウン記法

標準的なピタゴラスの五度連鎖記法は、アップ(^)とダウン(v)と一緒に使用できる。アップまたはダウンを1回行うと、音のピッチが1ステップ(1\22)変化する。

EbとD#は異なる音であり、かつEbのピッチはD#よりも低いことに注意せよ。これは硬い (en) ダイアトニックスケールの特徴である。

22平均律の記法
ステップ (en)	セント	アップ&ダウン記法 (en)
ステップ (en)	セント	ダイアトニック音程名 (en)	C始点の記号
0	0.00	完全1度(P1)	C
1	54.545	短2度 (m2) アップ1度 (^1)	Db ^C
2	109.091	アップ短2度 (^m2) ダウン増1度 (vA1) 減3度 (d3)	^Db vC# Ebb
3	163.636	ダウン長2度 (vM2) 増1度 (A1)	vD C#
4	218.182	長2度 (M2) アップ増1度 (^A1) ダウン短3度 (vm3)	D ^C# vEb
5	272.727	アップ長2度 (^M2) 短3度 (m3)	^D Eb
6	327.273	アップ短3度 (^m3) 減4度 (d4)	^Eb Fb
7	381.818	ダウン長3度 (vM3) 増2度 (A2) アップ減4度 (^d4)	vE D# ^Fb
8	436.364	長3度 (M3) アップ増2度 (^A2) ダウン4度 (v4)	E ^D# vFb
9	490.909	完全4度 (P4)	F
10	545.455	アップ4度 (^4) 減5度 (d5)	^F Gb
11	600.000	ダウン増4度 (vA4) アップ減5度 (^d5)	vF# ^Gb
12	654.545	増4度 (A4) ダウン5度 (v5)	F# vG
13	709.091	完全5度 (P5)	G
14	763.636	アップ5度 (^5) 短6度 (m6)	^G Ab
15	818.182	ダウン増5度 (vA5) アップ短6度 (^m6)	vG# ^Ab
16	872.727	増5度 (A5) ダウン長6度 (vM6)	G# vA
17	927.273	長6度 (M6) アップ増5度 (^A5) ダウン短7度 (vm7)	A ^G# vBb
18	981.818	短7度 (m7) アップ長6度 (^M6) ダウン減8度 (vd8)	Bb ^A vC
19	1036.364	アップ短7度 (^m7) 減8度 (d8)	^Bb Cb
20	1090.909	ダウン長7度 (vM7) アップ減8度 (^d8) 増6度 (A6)	vB ^Cb A#
21	1145.455	長7度 (M7) ダウン8度 (v8)	B vC
22	1200.000	完全8度 (P8)	C

アップ・ダウン記号 (en) をシャープ・フラットと「融合」したものとして扱い、別々に現れることはない記法の場合：

アップ・ダウン記号をシャープ・フラットとは独立したものとして扱い、別々に現れることもある記法の場合：

必須の臨時記号（調号なし）・最小限の臨時記号（調号を上書きする必要がある場合のみ）・独立したアップ・ダウン記号で、それぞれ表したDダウンメジャースケール。

あるいは、独立したアップ・ダウン記号の代わりに、Helmholtz–Ellis記法 (en) の矢印臨時記号を使用することもできる。

ステップオフセット	0	1	2	3	4	5	6	7
シャープ記号
フラット記号

下に示すのは独立したアップ・ダウン記号を用いて書かれたPaul Erlich (en) の “Tibia” in Gである。

Tibia in G (page 1)
Tibia in G (page 2)

22平均律の各記譜法の比較

ステップ数 (en)	セント	スーパーパイス/ポーキュパイン		ポーキュパイン			ペンタトニック			デカトニック			アップ&ダウン (en)			SKULO interval names (en)
0	0	ユニゾン	1	ユニゾン	P1	D	ユニゾン	P1	D	本位1度	N1	C	ユニゾン	P1	D	perfect unison	P1	D
1	55	s-短2度	sm2	増1度	A1	D#	増1度	A1	D#	変2度	f2	C#, δb	アップ1度, 短2度	^1, m2	^D, Eb	comma-wide unison, minor second	K1, m2	KD, Eb
2	109	p-減2度	pd2	減2度	d2	Eb	重増1度, 重減準3度	AA1, dds3	Dx, Fb³	本位2度	N2	δ	downaug 1sn, upminor 2nd	vA1, ^m2	vD#, ^Eb	classic minor 2nd	Km2	KEb
3	164	p-短2度	pm2	完全2度	P2	E	減準3度	ds3	Fbb	嬰2度, 変3度	s2, f3	δ#, Db	aug 1sn, downmajor 2nd	A1, vM2	D#, vE	classic/comma-narrow major 2nd	kM2	kE
4	218	(s/p)-長2度	M2	増2度	A2	E#	短準3度	ms3	Fb	本位3度	N3	D	major 2nd	M2	E	major 2nd	M2	E
5	273	s-短3度	sm3	減3度	d3	Fb	長準3度	Ms3	F	嬰3度	s3	D#	minor 3rd	m3	F	minor 3rd	m3	F
6	327	p-短3度	pm3	短3度	m3	F	増準3度	As3	F#	変4度	f4	εb	upminor 3rd	^m3	^F	classic minor 3rd	Km3	KF
7	382	p-長3度	pM3	長3度	M3	F#	重増準3度, 重減擬4度	AAs3, dd4d	Fx, Gbb	本位4度	N4	ε	downmajor 3rd	vM3	vF#	classic major 3rd	kM3	kF#
8	436	s-長3度	sM3	増3度, 減4度	A3, d4	Fx, Gb	減擬4度	d4d	Gb	嬰4度, 変5度	s4, f5	ε#, Eb	major 3rd	M3	F#	major 3rd	M3	F#
9	491	本位4度	4, N4	短4度	m4	G	完全擬4度	P4d	G	本位5度	N5	E	perfect 4th	P4	G	perfect 4th	P4	G
10	545	p-長4度, s-減5度	pM4, sd5	長4度	M4	G#	増擬4度	A4d	G#	嬰5度, 変6度	s5, f6	E#, γb	up-4th, dim 5th	^4, d5	^G, Ab	comma-wide 4th	K4	KG
11	600	p-増4度, p-減5度, 半オクターヴ	A4, HO	増4度, 減5度	A4, d5	Gx, Abb	重増擬4度, 重減擬5度	AA4d, dd5d	Gx, Abb	本位6度	N6	γ	downaug 4th, updim 5th	vA4, ^d5	vG#, ^Ab	comma-narrow augmented 4th comma-wide diminished 5th	kA4 Kd5	kG#, KAb
12	655	p-短5度, s-増4度	pm5, sA4	短5度	m5	Ab	減擬5度	d5d	Ab	嬰6度, 変7度	s6, f7	γ#, Gb	aug 4th, down-5th	A4, v5	G#, vA	comma-narrow 5th	k5	kA
13	709	本位5度	5, N5	長5度	M5	A	完全擬5度	P5d	A	本位7度	N7	G	perfect 5th	P5	A	perfect 5th	P5	A
14	764	s-短6度	sm6	増5度, 減6度	A5, d6	A#, Bbb	増擬5度	A5d	A#	嬰7度	s7	G#	minor 6th	m6	Bb	minor 6th	m6	Bb
15	818	p-短6度	pm6	短6度	m6	Bb	重増擬5度, 重減準7度	AA5d, dds7	Ax, Cb³	変8度	f8	αb	upminor 6th	^m6	^Bb	classic minor 6th	Km6	KBb
16	873	p-長6度	pM6	長6度	M6	B	減準7度	ds7	Cbb	本位8度	N8	α	downmajor 6th	vM6	vB	classic major 6th	kM6	kB
17	927	s-長6度	sM6	増6度	A6	B#	短準7度	ms7	Cb	嬰8度, 変9度	s8, f9	α#, Ab	major 6th	M6	B	major 6th	M6	B
18	982	(s/p)-短7度	m7	減7度	d7	Cb	長準7度	Ms7	C	本位9度	N9	A	minor 7th	m7	C	minor 7th	m7	C
19	1036	p-長7度	pM7	完全7度	P7	C	増準7度	As7	C#	嬰9度, 変10度	s9, f10	A#, βb	upminor 7th, dim 8ve	^m7, d8	^C, Db	classic minor 7th	Km7	kC
20	1091	p-増7度	pA7	増7度	A7	C#	重増準7度, 重減8度	AAs7, dd8	Cx, Dbb	本位10度	N10	β	downmajor 7th, updim 8ve	vM7, ^d8	vC#, ^Db	classic major 7th	kM7	kC#
21	1145	s-長7度	sM7	減8度	d8	Db	減8度	d8	Db	嬰10度	s10	β#, Cb	major 7th, down 8ve	M7, v8	C#, vD	major 7th / comma-narrow 8ve	M7 / k8	C#, kD
22	1200	オクターヴ	8	オクターヴ	P8	D	オクターヴ	P8	D	本位11度	N11	C	perfect octave	P8	D	perfect 8ve	P8	D

純正音程近似

15-奇数リミット音程のマッピング

以下の表は、22平均律で15奇数リミット音程がどのように表されるかを示している。素数倍音は太字で、非一貫的な音程は斜体で示す。

22平均律内の15奇数リミット音程（直接近似, 一貫性の無いものも含む）
音程と補音程	誤差 (絶対, ¢)	誤差 (相対, %)
1/1, 2/1	0.000	0.0
9/7, 14/9	1.280	2.3
11/10, 20/11	1.368	2.5
15/8, 16/15	2.640	4.8
5/4, 8/5	4.496	8.2
7/6, 12/7	5.856	10.7
11/8, 16/11	5.863	10.7
3/2, 4/3	7.136	13.1
15/11, 22/15	8.504	15.6
15/14, 28/15	10.352	19.0
5/3, 6/5	11.631	21.3
7/4, 8/7	12.992	23.8
11/6, 12/11	12.999	23.8
9/8, 16/9	14.272	26.2
13/11, 22/13	16.482	30.2
7/5, 10/7	17.488	32.1
13/10, 20/13	17.850	32.7
13/9, 18/13	17.928	32.9
9/5, 10/9	18.767	34.4
11/7, 14/11	18.856	34.6
13/7, 14/13	19.207	35.2
11/9, 18/11	20.135	36.9
13/8, 16/13	22.346	41.0
15/13, 26/15	24.986	45.8
13/12, 24/13	25.064	46.0

22平均律内の15奇数リミット音程（パテントヴァルによるマッピング）
音程と補音程	誤差 (絶対, ¢)	誤差 (相対, %)
1/1, 2/1	0.000	0.0
9/7, 14/9	1.280	2.3
11/10, 20/11	1.368	2.5
15/8, 16/15	2.640	4.8
5/4, 8/5	4.496	8.2
7/6, 12/7	5.856	10.7
11/8, 16/11	5.863	10.7
3/2, 4/3	7.136	13.1
15/11, 22/15	8.504	15.6
15/14, 28/15	10.352	19.0
5/3, 6/5	11.631	21.3
7/4, 8/7	12.992	23.8
11/6, 12/11	12.999	23.8
9/8, 16/9	14.272	26.2
13/11, 22/13	16.482	30.2
7/5, 10/7	17.488	32.1
13/10, 20/13	17.850	32.7
9/5, 10/9	18.767	34.4
11/7, 14/11	18.856	34.6
11/9, 18/11	20.135	36.9
13/8, 16/13	22.346	41.0
15/13, 26/15	24.986	45.8
13/12, 24/13	29.482	54.0
13/7, 14/13	35.338	64.8
13/9, 18/13	36.618	67.1

22平均律で近似されるいくつかの17-リミット音程

決定づける特徴

アルキュタス vs シントニックコンマ

おそらく、22平均律に慣れていない人にとって最も印象的な特徴は、81/80 のシントニックコンマをテンパーアウトしないため、ミーントーン音律のシステムではないことである。つまり、22平均律は、9/8 と 10/9 の2つの全音などの、12平均律・19平均律・31平均律が区別しないピタゴラス(3-リミット)音程と5-リミット音程を区別する。実際、これらの区別は、5-リミット純正律(JI)や、34平均律 (en) ・41平均律 (en) ・53平均律などのより正確な音律と比較すると誇張されている。

22 平均律が作り出すダイアトニックスケールはスーパーパイス (en) 音律から派生したもので、ミーントーンのダイアトニックスケール（LLsLLLs, または 5L 2s）と同じスケール構造を持ちながらも、3度は 5/4 や 6/5 ではなく、9/7 や 7/6 に近い。つまり、シントニックコンマ(81/80)ではなく、アルキュタスコンマ(64/63)が消えるということであり、これは22平均律の核となる特徴の一つである。スーパーパイスは、疑似的に等間隔の5音階（大全音と下短(縮)3度の大きさがかなり近いため）と、12平均律やその他のミーントーンシステムと比べ、より不均等な7音階を持つ点で旋律的に興味深い。ステップパターンはそれぞれ 4 4 5 4 5 と 4 4 1 4 4 4 1 である。

ポーキュパインコンマ

また、250/243 (en) のポーキュパインコンマ（或いはmaximal diesis）をテンパーアウトするため、22平均律はポーキュパイン音律 (en) をサポート (en) する。ポーキュパインのジェネレーターは低い 10/9 の小全音で、2つでわずかに高い 6/5、3つでわずかに低い 4/3 になる。これは、ポーキュパインの特徴である等間隔なテトラコルドの存在を示唆している。ポーキュパインは、良く知られた12平均律によっては近似されない5-リミット音律のうち、悪さ (en) (badness)が最も少ないものであることで有名である。そのため、22平均律の倍音特性を調べるための優れた出発点の一つとなる。ポーキュパインは7音と8音の二つのMOSスケールを形成し、22平均律ではそれぞれ 4 3 3 3 3 3 と 3 1 3 3 3 3 3 3（およびそれぞれのモード）に調律される。

その他の5-リミットコンマ

22平均律がテンパーアウトするその他の5-リミットコンマには、ディアスキスマ（diaschisma, 2048/2025 (en) ）とマジックコンマ（或いはsmall diesis, 3125/3072 (en) ）がある。12平均律や22平均律などのディアスキスマシステムでは、全音階の3度上の 9/8 (en) を表す大全音の長3度上である 45/32 (en) のダイアトニック三全音は、そのオクターヴ反転である 64/45 (en) と等しくなる。また、マジックコンマがテンパーアウトされるということは、22平均律が5つの長3度で完全5度を構成するマジックシステムであることを意味する。

その他の7-リミットコンマ

7-リミットでは、22平均律は12平均律によってもテンパーアウトされる特定のコンマをテンパーアウトする。これは、ミーントーンシステムが類似するのとは異なる方法で12平均律を22平均律に関連付ける。jubilisma(50/49 (en) )とアルキュタスコンマ (64/63) は、両方のシステムでテンパーアウトされる。したがってどちらの平均律においても、50/49 により 7/5 と 10/7 の2つの7倍音系三全音が同一視され、さらに 64/63 により属七和音とotonalテトラッドが区別されない。したがって、どちらも (50/49)/(64/63) = 225/224 (en) のマーベルコンマ（或いはセプティマルクレイズマ）をテンパーアウトするため、マーベル増三和音は22平均律のコードであり、どのミーントーン調律のコードでもある。12平均律によってテンパーアウトされないが、22平均律によってテンパーアウトされる7倍音系コンマは 1728/1715、つまりオーウェルコンマ (en) である。また、オーウェル四和音 (en) も22平均律のコードである。

11-リミットコンマ

11-リミットでは、22平均律はen:quartismaをテンパーアウトし、5つの 33/32 四分音が1つの 7/6 下短(縮)3度に等しくなる。これは24平均律と共有されている特性だが、驚くべきことに、17平均律・26平均律 (en) ・34平均律 (en) などの他の比較的小さな平均律のいくつかと共有されてはいない。実際、有名な53平均律でさえこの特性を持っていない。ただし、関連する159平均律にはあることに注意。

その他の特徴

164 ¢ の「低い小全音」は、22平均律の重要な音程である。これは、11-リミットで 10/9, 11/10, 12/11 という3つもの異なる協和音程比として機能するためである。したがって、非常に曖昧でかつ柔軟性がある。その代償として、12平均律ピアノの中間に非常に近いため、ほとんどの12平均律のリスナーにとっては慣れるのに時間がかかる。5-リミットの音楽を22平均律に単純に変換すると、非常に異なるサウンドになり、より複雑な倍音のクオリティが必然的に生じる。22平均律には中立3度は含まれないが、5-リミットの3度は両方とも「中立のような」クオリティを持つ。これは、12平均律のように離れているのではなく、より近い距離で調律されているためである。

22平均律は、7倍音系下短3度をジェネレーター（5ステップ）として使用し、ステップパターン 3 2 3 2 3 2 3 2 2 および 1 2 2 1 2 2 1 2 2 1 2 2 2 でMOSスケールを形成するオーウェル音律もサポートしている。ハーモニー的には、オーウェルは31平均律・53平均律・84平均律 (en) など、他の音律でより正確にチューニングできる。しかし、22平均律オーウェルはメロディ的に他よりも優位に立っており、オーウェル[9]の大小のステップは22では区別しやすい。

22平均律は、4分音と短2度・中立2度・長2度を含む点で24平均律と旋律的に似ているが、22平均律は24よりも総合的に優れたハーモニーを提供する。サジタルノーテーション (en) では、11は22の他のすべての音符として記譜できる。

レギュラー音律の性質

サブグループ (en)	コンマリスト (en)	マッピング (en)	最適なオクターヴ伸縮 (¢)	調律誤差
サブグループ (en)	コンマリスト (en)	マッピング (en)	最適なオクターヴ伸縮 (¢)	絶対 (¢)	相対 (%)
2.3	[35 -22⟩	[⟨22 35]]	-2.25	2.25	4.12
2.3.5	250/243, 2048/2025	[⟨22 35 51]]	-0.86	2.70	4.94
2.3.5.7	50/49, 64/63, 245/243	[⟨22 35 51 62]]	-1.80	2.85	5.23
2.3.5.7.11	50/49, 55/54, 64/63, 99/98	[⟨22 35 51 62 76]]	-1.11	2.90	5.33
2.3.5.7.11.17	50/49, 55/54, 64/63, 85/84, 99/98	[⟨22 35 51 62 76 90]]	-1.09	2.65	4.87

22平均律は、11-リミットにおけるこれまでのどの平均律よりも相対誤差が低くなる。このサブグループで優れている次の平均律は31平均律である。22平均律は 2.3.5.7.11.17 サブグループでさらに卓越しており、このサブグループで優れている次の平均律は46平均律 (en) である。

一様写像

21.5と22.5の間の13リミット一様写像
最小サイズ	最大サイズ	Wart記法	Map
21.5000	21.5353	22bccdddeeeeff	⟨22 34 50 60 74 80]
21.5353	21.5505	22bccdddeeff	⟨22 34 50 60 75 80]
21.5505	21.7492	22bccdeeff	⟨22 34 50 61 75 80]
21.7492	21.7542	22bdeeff	⟨22 34 51 61 75 80]
21.7542	21.7671	22bdee	⟨22 34 51 61 75 81]
21.7671	21.8244	22dee	⟨22 35 51 61 75 81]
21.8244	21.9067	22d	⟨22 35 51 61 76 81]
21.9067	22.0244	22	⟨22 35 51 62 76 81]
22.0244	22.1135	22f	⟨22 35 51 62 76 82]
22.1135	22.1798	22ef	⟨22 35 51 62 77 82]
22.1798	22.2629	22cef	⟨22 35 52 62 77 82]
22.2629	22.2946	22cddef	⟨22 35 52 63 77 82]
22.2946	22.3980	22cddefff	⟨22 35 52 63 77 83]
22.3980	22.4025	22bbcddefff	⟨22 36 52 63 77 83]
22.4025	22.5000	22bbcddeeefff	⟨22 36 52 63 78 83]

コンマ

22平均律は以下のコンマをテンパーアウト (en) する（ヴァルは ⟨22 35 51 62 76 81] とする。）

素数リミット (en)	比率^[1]	モンゾ	セント	カラーネーム (en)	名前
3	(22 digits)	[35 -22⟩	156.98
5	250/243	[1 -5 3⟩	49.17	Triyo	Porcupine comma
5	3125/3072	[-10 -1 5⟩	29.61	Laquinyo	Magic comma
5	2048/2025	[11 -4 -2⟩	19.55	Sagugu	Diaschisma
5	(14 digits)	[-21 3 7⟩	10.06	Lasepyo	Semicomma
5	(20 digits)	[32 -7 -9⟩	9.49	Sasa-tritrigu	Escapade comma
5	(32 digits)	[-53 10 16⟩	0.57	Quadla-quadquadyo	Kwazy
7	50/49	[1 0 2 -2⟩	34.98	Biruyo	Jubilisma
7	64/63	[6 -2 0 -1⟩	27.26	Ru	Septimal comma
7	875/864	[-5 -3 3 1⟩	21.90	Zotriyo	Keema
7	2430/2401	[1 5 1 -4⟩	20.79	Quadru-ayo	Nuwell
7	245/243	[0 -5 1 2⟩	14.19	Zozoyo	Sensamagic
7	1728/1715	[6 3 -1 -3⟩	13.07	Triru-agu	Orwellisma
7	225/224	[-5 2 2 -1⟩	7.71	Ruyoyo	Marvel comma
7	10976/10935	[5 -7 -1 3⟩	6.48	Trizo-agu	Hemimage
7	6144/6125	[11 1 -3 -2⟩	5.36	Saruru-atrigu	Porwell
7	65625/65536	[-16 1 5 1⟩	2.35	Lazoquinyo	Horwell
7	(12 digits)	[-6 -8 2 5⟩	1.12	Quinzo-ayoyo	Wizma
11	99/98	[-1 2 0 -2 1⟩	17.58	Loruru	Mothwellsma
11	100/99	[2 -2 2 0 -1⟩	17.40	Luyoyo	Ptolemisma
11	121/120	[-3 -1 -1 0 2⟩	14.37	Lologu	Biyatisma
11	176/175	[4 0 -2 -1 1⟩	9.86	Lorugugu	Valinorsma
11	896/891	[7 -4 0 1 -1⟩	9.69	Saluzo	Pentacircle
11	65536/65219	[16 0 0 -2 -3⟩	8.39	Satrilu-aruru	Orgonisma
11	385/384	[-7 -1 1 1 1⟩	4.50	Lozoyo	Keenanisma
11	540/539	[2 3 1 -2 -1⟩	3.21	Lururuyo	Swetisma
11	4000/3993	[5 -1 3 0 -3⟩	3.03	Triluyo	Wizardharry
11	9801/9800	[-3 4 -2 -2 2⟩	0.18	Bilorugu	Kalisma
13	65/64	[-6 0 1 0 0 1⟩	26.84	Thoyo	Wilsorma
13	78/77	[1 1 0 -1 -1 1⟩	22.34	Tholuru	Negustma
13	91/90	[-1 -2 -1 1 0 1⟩	19.13	Thozogu	Superleap
31	125/124	[-2 0 3 0 0 0 0 0 0 0 -1⟩	13.91	Thiwutriyo	Twizzler

↑ 10桁以上の比率は、ヒントを含むプレースホルダーによって示す。

ランク-2 音律

Periods per octave	Generator	Temperaments
1	1\22	Sensa Chromo Ceratitid
1	3\22	Porcupine
1	5\22	Orwell (22) / blair (22) / winston (22f)
1	7\22	Magic / telepathy
1	9\22	Superpyth / suprapyth
2	1\22	Shrutar / hemipaj Comic
2	2\22	Srutal / pajara / pajarous
2	3\22	Hedgehog / echidna
2	4\22	Astrology Antikythera Wizard
2	5\22	Doublewide / fleetwood
11	1\22	Undeka Hendecatonic

スケール

en:22edo modesを参照のこと。

テトラコルド

en:22edo tetrachordsを参照のこと。

コードネーム

アップ&ダウン記法とカラー記法 (en) を組み合わせると、次のようにクオリティをカラーと大まかに関連付けることができる。

クオリティ	カラーネーム (en)	モンゾ形式	例
短	zo	[a b 0 1⟩	7/6, 7/4
短	fourthward wa	[a b⟩ (b < -1)	32/27, 16/9
アップ短	gu	[a b -1⟩	6/5, 9/5
ダウン長	yo	[a b 1⟩	5/4, 5/3
長	fifthward wa	[a b⟩ (b > 1)	9/8, 27/16
長	ru	[a b 0 -1⟩	9/7, 12/7

すべての22平均律の和音は、アップ&ダウンを使用して名前を付けることができる。変位音は常に括弧で囲まれるが、追加音は括弧で囲まれない。コード根音の直後のアップ・ダウンは、3度、6度、7度、および11度（3度堆積和音 6-1-3-5-7-9-11-13 の一つおきの音）に影響する。zo, gu, yo, ruの三和音は次のとおり。

3度のカラー (en)	純正比	ステップ	C上における音	表記	読み方
zo	6:7:9	0-5-13	C Eb G	Cm	Cマイナー
gu	10:12:15	0-6-13	C ^Eb G	C^m	Cアップマイナー
yo	4:5:6	0-7-13	C vE G	Cv	Cダウンメジャー, Cダウン
ru	14:18:21	0-8-13	C E G	C	Cメジャー, C

例：

0-4-13 = C D G = C2
0-9-13 = C F G = C4
0-10-13 = C ^F G = C^4 or C(^4)
0-5-10 = C Eb Gb = Cd = Cdim
0-5-11 = C Eb ^Gb = Cd(^5)
0-5-12 = C Eb vG = Cm(v5)

22平均律の和音の名前に関するより深い議論はこちらを参照。

音楽

en:22edo/musicsやen:category:22edo tracksを参照のこと。

外部リンク

参考文献

Barbour, James Murray, Tuning and temperament, a historical survey, East Lansing, Michigan State College Press, 1953 [c1951]
Bosanquet, R.H.M. On the Hindoo division of the octave, with additions to the theory of higher orders, Proceedings of the Royal Society of London vol. 26, 1879, pp. 272-284. Reproduced in Tagore, Sourindro Mohun, Hindu Music from Various Authors, Chowkhamba Sanskrit Series, Varanasi, India, 1965

[1] 22平均律を2.3.5.7.11.17サブグループ音律として扱うことに基づいて、サイズの大きい順に並べられたいくつかの単純な比率。他のアプローチも可能。

[2] 10桁以上の比率は、ヒントを含むプレースホルダーによって示す。

[1]

[1]